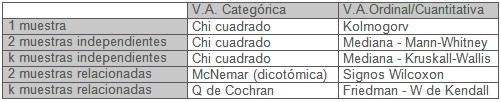
En ciencias biológicas la mayor parte de las variables sigue una distribución normal, lo cual facilita en extremo el uso de la mayor parte de las técnicas estadísticas; no obstante es labor nuestra asegurarnos y confirmar que, efectivamente, las variables que vamos a utilizar en nuestros análisis siguen dicha distribución normal y, en caso contrario, tendremos que recurrir a los denominados contrastes no paramétricos. En este capítulo nos ocuparemos primero de los contrastes que nos permiten conocer si una variable se distribuye o no de un modo normal y, a continuación, veremos cuáles son los principales test no paramétricos que podría utilizar en función de las comparaciones que deseemos realizar. En la tabla siguiente representamos los principales test no paramétricos, o cuando menos, los de uso más frecuente.
Test no paramétricos para datos biosanitarios con SPSS
Juan Manuel García Torrecillas. Médico de Familia del SCUU del CH Torrecárdenas. Almería.
Herminia Moreno Martos: Técnico de Salud. Unidad Docente de Medicina Familiar y Comunitaria. Almería.
María del Carmen Lea Pereira. FEA en Medicina Interna. Empresa Pública Hospital de Poniente. El Ejido. Almería.
En ciencias biológicas la mayor parte de las variables sigue una distribución normal, lo cual facilita en extremo el uso de la mayor parte de las técnicas estadísticas; no obstante es labor nuestra asegurarnos y confirmar que, efectivamente, las variables que vamos a utilizar en nuestros análisis siguen dicha distribución normal y, en caso contrario, tendremos que recurrir a los denominados contrastes no paramétricos.
En este capítulo nos ocuparemos primero de los contrastes que nos permiten conocer si una variable se distribuye o no de un modo normal y, a continuación, veremos cuáles son los principales test no paramétricos que podría utilizar en función de las comparaciones que deseemos realizar. En la tabla siguiente representamos los principales test no paramétricos, o cuando menos, los de uso más frecuente.
7.1. TEST DE KOLMOGOROV-SMIRNOV
Este test pretende permitirnos conocer si una variable se distribuye de un modo normal, lo cual nos permitirá posteriormente elegir adecuadamente los contrastes a utilizar aunque, en sentido estricto, también nos daría información de si la distribución de datos se ajusta a otras como una Poisson, uniforme, etc.
En primer lugar seleccionamos AnalizaràPruebas no paramétricasà K-S de 1 muestra lo que nos da paso al cuadro de diálogo que exponemos en la figura.
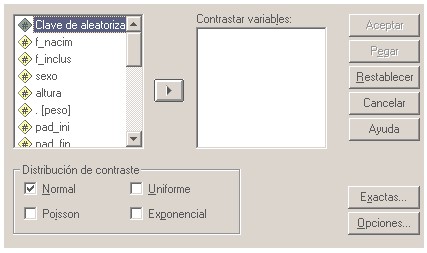
Como vemos se trata de contrastar la distribución de datos de nuestra variable, con las diferentes opciones que nos brinda SPSS, que abajo y a la izquierda en el cuadro de diálogo, son la Normal, Poisson, Uniforme o Exponencial. Pasamos a la caja de "contrastar variable" aquella que queremos que sea examinada, en nuestro caso podríamos introducir y, de no indicar nada, por defecto el contraste lo realiza sobre la Normal.
El contraste que realizamos es H0ºla variable a examen y la variable normal no difieren en su distribución vs H1ºla variable a examen y la variable normal sí difieren en su distribución; por tanto, si en la significación asintótica (bilateral) que obtendremos en los resultados obtenemos una p<0.05 concluiremos H1 y diremos que no se distribuye siguiendo la normal. Si por el contrario obtenemos para la/s variable/s significaciones > 0.05 entonces sí que podemos trabajar con ellas con la tranquilidad de que siguen una distribución normal.
Si queremos saber en nuestro ejemplo si siguen una distribución normal las variables altura, edad, número de cigarrillos e índice de masa corporal, las incluimos en el cuadro de diálogo de "contrastar variables" como vimos más arriba, dejando marcada la opción "normal" que viene por defecto y obtenemos el siguiente resultado:
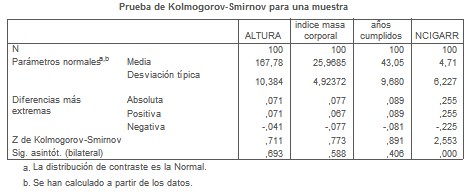
Observamos que la significación bilateral para las tres variables es mayor de 0.05, del nivel crítico, por tanto se distribuyen de un modo normal todas excepto la variable "número de cigarrillos".
7.2 TEST DE MANN-WHITNEY
Para comparar dos muestras independientes cuando estas no siguen una distribución normal y estas son de tipo cuantitativo u ordinal, usaremos el test no paramétrico de Mann-Whitney
Supongamos que deseamos conocer si hay diferencias en el número de cigarrillos fumados en función del sexo. Se trata de comparar dos muestras independientes pero donde la variable a contrastar "numero de cigarrillos" sabemos que no sigue una distribución normal. Para ello AnalizaràPruebas no paramétricasà2 muestras independientes, y obtenemos el cuadro de diálogo siguiente, introduciendo las variable número de cigarrillos en la caja "contraste de variables" y la variable de agrupación que en nuestro caso es el sexo, no olvidando definir los grupos, en este caso sexo, según los valores 0 y 1 que asignamos inicialmente:
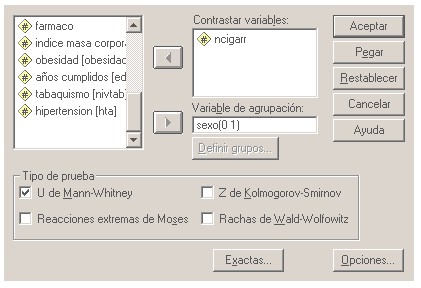
Notemos que además de la U de Mann-Whitney podemos seleccionar otros contrastes no paramétricos como la Z de Kolmogorov Smirnov o el test de Rachas de Wald Wolfowitz, etc. El resultado obtenido al ejecutar el cuadro de diálogo anterior es el siguiente:
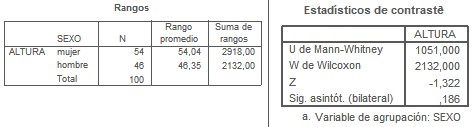
Como el nivel crítico, la significación asintótica bilateral obtenida (0.186) es mayor de 0.05 concluimos H0, esto es, no hay diferencias en el número de cigarrillos en ambos grupos. Como observamos el procedimiento está basado (observemos la tabla de la izquierda) en calcular las medias de los rangos para cada muestra y posteriormente el programa contabiliza el número de veces que preceden los rangos de una muestra a los de la otra.
7.3 TEST DE WILCOXON
Si deseamos comparar dos muestras relacionadas o pares de variables cuantitativas u ordinales, realizaremos el test de Wilcoxon. Especificamos la secuencia de orden Analizar à Pruebas no paramétricas à 2 muestras relacionadas y accedemos al siguiente cuadro de diálogo:
Vemos que también nos permite realizar el test de Signos y el McNemar. El Test de signos básicamente contabiliza el número de diferencias que se dan entre ambas variables, tanto positivas como negativas, y a partir de su diferencia proporciona la comparación entre ambas. El Mc Nemar lo estudiaremos en el próximo apartado.
Retomando nuestro ejemplo, si deseamos contrastar la presión arterial sistólica inicial y final (suponiendo que fueran variables de distribución no normal), las introduciríamos en la caja de "contrastar pares" y obtendríamos el siguiente resultado:
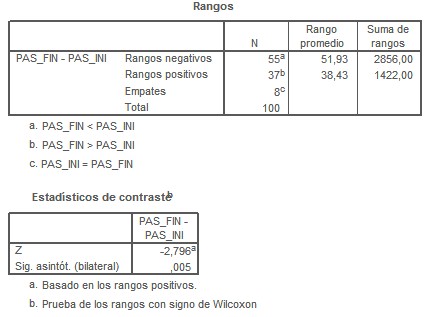
En la ventana de resultados podemos ver el número de empates y rangos, así como la significación; en este caso concreto concluimos H1, esto es, hay diferencias entre las variables analizadas por pares en este caso.
7.4. TEST DE McNEMAR
Cuando las variables a contrastar son dicotómicas podemos usar el test de McNemar (sólo en este caso), permitiéndonos pues la comparación de frecuencias y porcentajes obtenidos de dichas variables. Suponiendo en nuestro ejemplo que la variable obesidad no siguiera una distribución normal, la comparación para determinar si la proporción de obesos antes y después de un tratamiento difiere, podría hacerse mediante este test.
7.5. TEST DE KRUSKAL-WALLIS
Se utiliza para la comparación de varias muestras con objeto de determinar si proceden o no de la misma población, cuando se consideran como independientes.